Decoding The Okay-Means Clustering Algorithm: A Deep Dive Into Its Flowchart And Implementation

Decoding the Okay-Means Clustering Algorithm: A Deep Dive into its Flowchart and Implementation

Associated Articles: Decoding the Okay-Means Clustering Algorithm: A Deep Dive into its Flowchart and Implementation

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to Decoding the Okay-Means Clustering Algorithm: A Deep Dive into its Flowchart and Implementation. Let’s weave attention-grabbing info and supply contemporary views to the readers.

Decoding the Okay-Means Clustering Algorithm: A Deep Dive into its Flowchart and Implementation

Okay-means clustering is a elementary unsupervised machine studying algorithm used to partition a dataset into ok distinct clusters, the place every information level belongs to the cluster with the closest imply (centroid). Its simplicity and effectivity make it a well-liked selection for numerous functions, starting from buyer segmentation and picture compression to anomaly detection and doc classification. Understanding the algorithm’s interior workings is essential for efficient software and interpretation of outcomes. This text supplies a complete exploration of the Okay-means algorithm, specializing in its flowchart illustration and an in depth breakdown of every step.

The Core Idea: Minimizing Inside-Cluster Variance

The first purpose of Okay-means is to reduce the sum of squared distances between every information level and the centroid of its assigned cluster. That is sometimes called minimizing the within-cluster variance or inertia. The algorithm iteratively refines cluster assignments till this variance is minimized (or a predefined convergence criterion is met). The effectiveness of Okay-means closely depends upon the preliminary placement of centroids and the selection of the variety of clusters (ok).

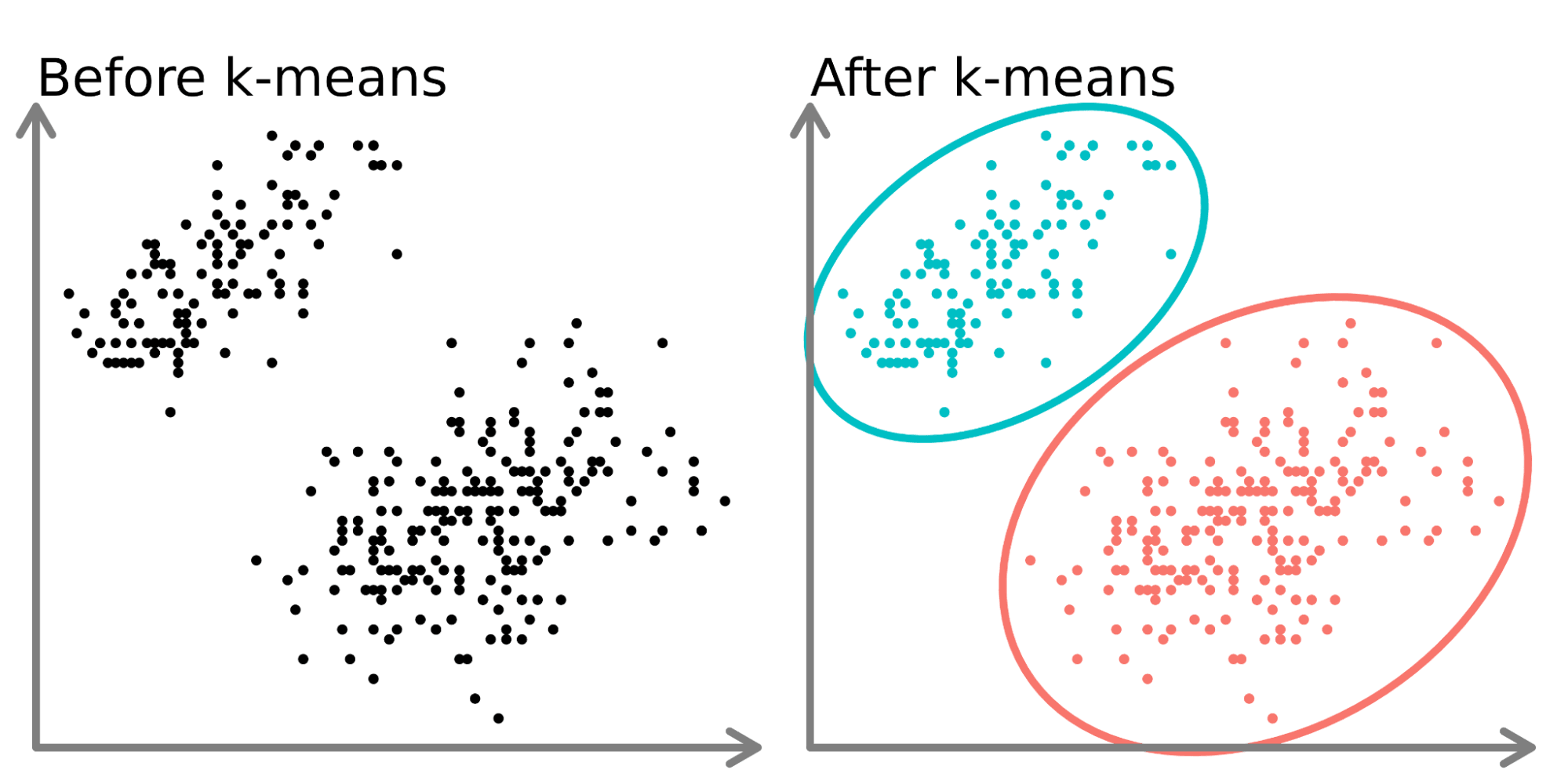
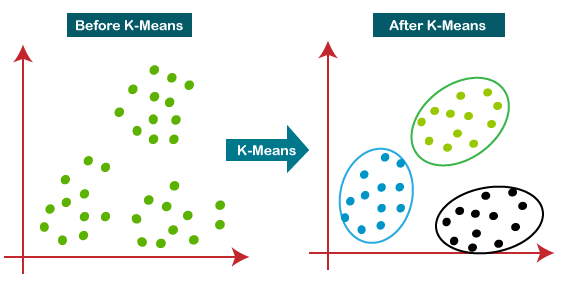
The Flowchart: A Visible Illustration of the Algorithm

The flowchart beneath supplies a visible illustration of the Okay-means algorithm’s iterative course of. Every step is then defined intimately within the subsequent sections.

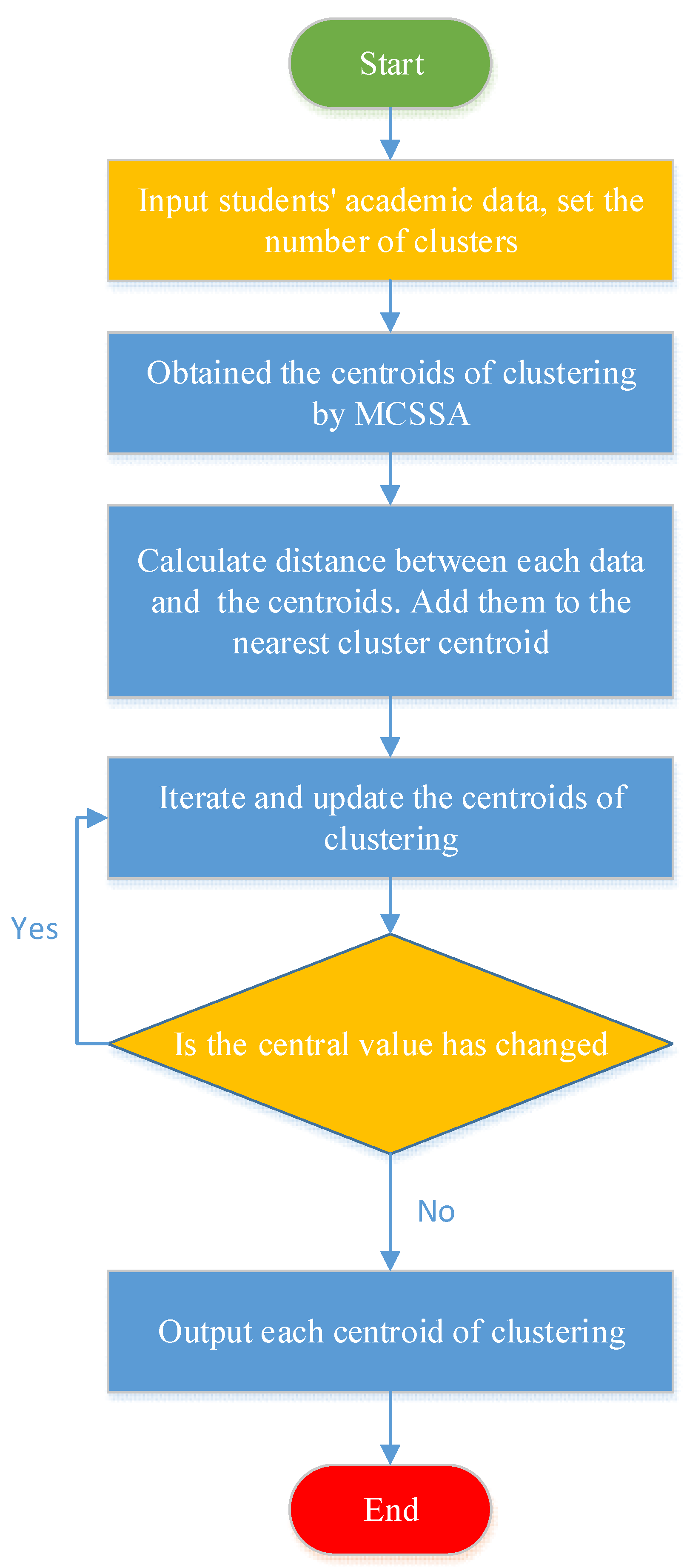
[Start] --> [Initialize k centroids randomly] --> [Assign each data point to the nearest centroid] --> [Calculate new centroids as the mean of the points in each cluster] --> [Check for convergence (e.g., centroid movement below a threshold or maximum iterations reached)] --> [Yes: Output clusters] --> [No: Go back to "Assign each data point to the nearest centroid"] --> [End]

1. Initialization: The Essential First Step

The algorithm begins by randomly initializing ok centroids. These centroids symbolize the preliminary guess for the middle of every cluster. The selection of initialization technique can considerably affect the ultimate clustering outcome. A number of methods exist:

• Random Initialization: The only technique, the place centroids are randomly chosen from the dataset. This strategy can result in suboptimal options, notably with advanced datasets. A number of runs with completely different random initializations are sometimes essential to mitigate this problem.
• Okay-Means++: A extra subtle strategy designed to enhance the preliminary centroid placement. It goals to distribute centroids extra strategically, decreasing the probability of getting caught in native optima. The algorithm selects the primary centroid randomly, then iteratively selects subsequent centroids primarily based on their distance from current centroids, favoring factors additional away.
• Forgy Methodology: This technique randomly selects ok information factors from the dataset as preliminary centroids.

The standard of the preliminary centroid placement immediately influences the convergence pace and the ultimate clustering resolution. Poor initialization may end up in clusters which might be poorly separated or don’t replicate the true underlying construction of the info.

2. Project Step: Discovering the Closest Centroid

As soon as the centroids are initialized, every information level within the dataset is assigned to the closest centroid primarily based on a selected distance metric. The commonest metric is Euclidean distance, calculated as:

distance = sqrt((x1 - x2)^2 + (y1 - y2)^2 + ... + (xn - xn)^2)

the place (x1, y1, …, xn) and (x2, y2, …, xn) symbolize the coordinates of two information factors in n-dimensional area. Different distance metrics, corresponding to Manhattan distance or Minkowski distance, can be used relying on the particular software and information traits.

This project step creates a preliminary partitioning of the info into ok clusters. Every information level is assigned to the cluster whose centroid is closest to it.

3. Replace Step: Recalculating Centroids

After assigning all information factors to clusters, the algorithm recalculates the centroids for every cluster. The brand new centroid for every cluster is solely the imply (common) of all information factors assigned to that cluster. This step adjusts the cluster facilities primarily based on the present information level assignments.

4. Convergence Examine: Iterating In the direction of Optimality

The algorithm iteratively repeats steps 2 and three till a convergence criterion is met. Widespread convergence standards embrace:

• Most Iterations: The algorithm terminates after a predefined variety of iterations, even when the centroids have not totally converged.
• Centroid Motion Threshold: The algorithm stops when the change in centroid positions between iterations falls beneath a predefined threshold. This means that the clusters have stabilized.
• Inertia Change Threshold: The algorithm terminates when the change within the within-cluster variance (inertia) between iterations is beneath a predefined threshold. This measures the general enchancment in cluster high quality.

The selection of convergence criterion depends upon the particular software and desired degree of accuracy. Utilizing a number of standards can present a extra strong stopping situation.

5. Output: The Remaining Clusters

As soon as the algorithm converges, it outputs the ultimate ok clusters, together with their respective centroids. Every information level is assigned to a single cluster, and the centroids symbolize the central tendency of every cluster. These outcomes can then be used for additional evaluation, visualization, or decision-making.

Challenges and Limitations of Okay-Means Clustering

Regardless of its simplicity and effectiveness, Okay-means has a number of limitations:

• Sensitivity to Preliminary Centroids: As talked about earlier, the selection of preliminary centroids can considerably affect the ultimate clustering outcome. A number of runs with completely different initializations are sometimes advisable to mitigate this problem.
• Issue with Non-Spherical Clusters: Okay-means assumes clusters are spherical or at the least roughly spherical. It struggles with clusters of arbitrary shapes or sizes.
• Sensitivity to Outliers: Outliers can considerably affect the place of centroids, resulting in distorted clusters. Preprocessing methods to deal with outliers are sometimes obligatory.
• Figuring out the Optimum ok: Selecting the optimum variety of clusters (ok) is a vital side of Okay-means. Strategies just like the elbow technique, silhouette evaluation, or the hole statistic can assist decide an appropriate worth for ok.
• Computational Complexity: Whereas comparatively environment friendly for smaller datasets, Okay-means can develop into computationally costly for very massive datasets with excessive dimensionality.

Superior Methods and Extensions

A number of methods have been developed to deal with the restrictions of normal Okay-means:

• Okay-medoids: This algorithm makes use of precise information factors as centroids as an alternative of means, making it extra strong to outliers.
• Kernel Okay-means: This extends Okay-means to deal with non-linearly separable information by mapping the info right into a higher-dimensional area utilizing kernel features.
• Mini-Batch Okay-means: This algorithm makes use of smaller batches of information factors to replace centroids, making it extra environment friendly for giant datasets.

Conclusion:

Okay-means clustering is a strong and versatile algorithm for partitioning information into significant clusters. Understanding its flowchart, the iterative course of, and its limitations is essential for efficient software. Whereas it has sure drawbacks, the simplicity, effectivity, and vast applicability of Okay-means make it a elementary software within the machine studying practitioner’s arsenal. By rigorously contemplating initialization methods, convergence standards, and potential limitations, one can successfully leverage Okay-means for quite a lot of information evaluation and machine studying duties. Additional analysis into superior methods and extensions can assist tackle a few of its shortcomings and enhance its efficiency on advanced datasets.

Closure

Thus, we hope this text has offered invaluable insights into Decoding the Okay-Means Clustering Algorithm: A Deep Dive into its Flowchart and Implementation. We thanks for taking the time to learn this text. See you in our subsequent article!