Navigating the Metric System: A Complete Information to Models of Measurement
Associated Articles: Navigating the Metric System: A Complete Information to Models of Measurement
Introduction
On this auspicious event, we’re delighted to delve into the intriguing matter associated to Navigating the Metric System: A Complete Information to Models of Measurement. Let’s weave fascinating info and supply contemporary views to the readers.
Desk of Content material
Navigating the Metric System: A Complete Information to Models of Measurement
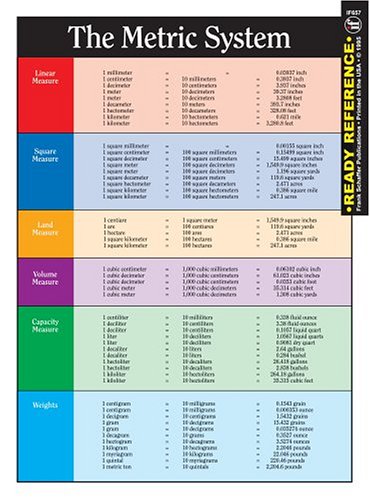
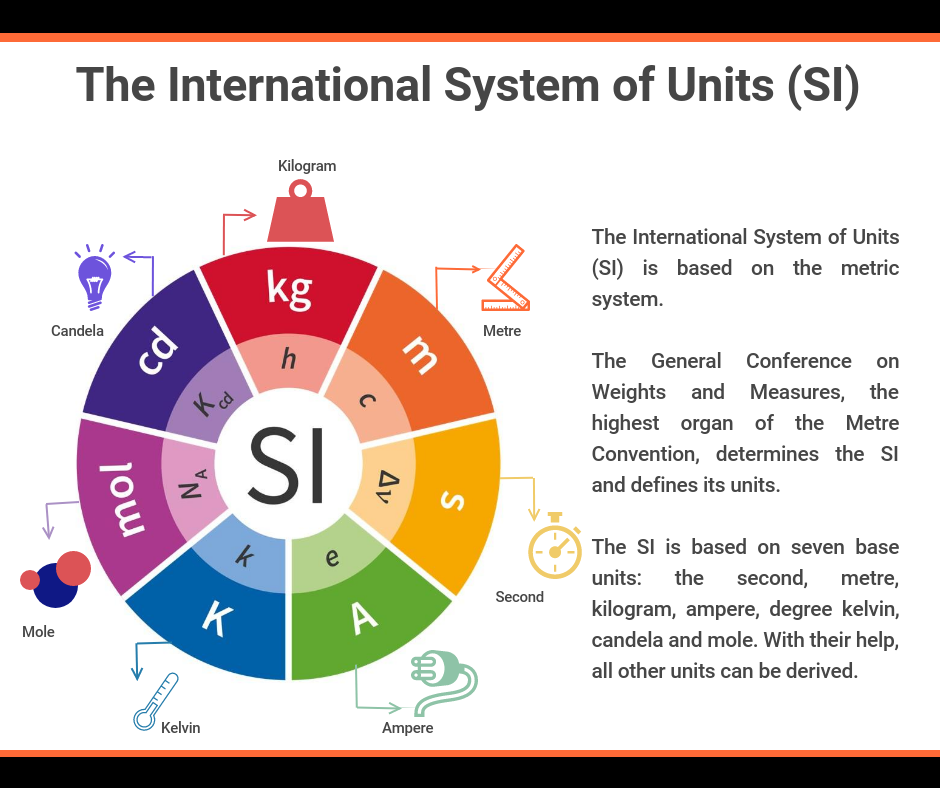
The metric system, formally often called the Worldwide System of Models (SI), is a decimal system of measurement based mostly on models of ten. Its widespread adoption globally stems from its simplicity and ease of conversion between models. Not like the imperial system, which depends on arbitrary models and complicated conversion elements, the metric system makes use of prefixes to point multiples or fractions of base models. This text delves into the generally used metric models for size, quantity, and mass, offering a complete understanding by charts, explanations, and sensible examples.
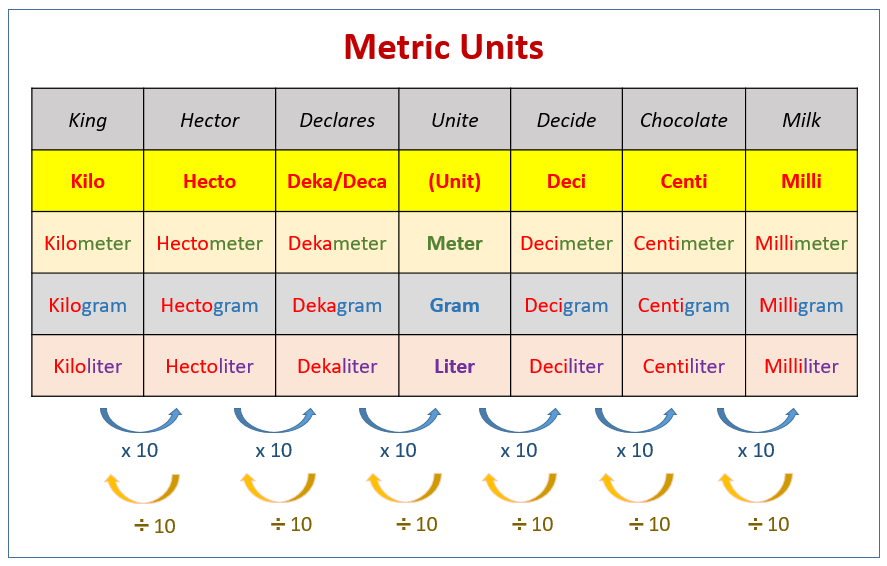
I. Understanding the Metric Prefixes:
Earlier than diving into particular models, it is essential to understand the core of the metric system: its prefixes. These prefixes, positioned earlier than the bottom unit, denote an influence of ten. This is a desk summarizing essentially the most ceaselessly used prefixes:
| Prefix | Image | Multiplier |
|---|---|---|
| Giga | G | 1,000,000,000 (10⁹) |
| Mega | M | 1,000,000 (10⁶) |
| Kilo | ok | 1,000 (10³) |
| Hecto | h | 100 (10²) |
| Deka | da | 10 (10¹) |
| Base Unit | 1 (10⁰) | |
| Deci | d | 0.1 (10⁻¹) |
| Centi | c | 0.01 (10⁻²) |
| Milli | m | 0.001 (10⁻³) |
| Micro | µ | 0.000001 (10⁻⁶) |
| Nano | n | 0.000000001 (10⁻⁹) |
This desk is prime to understanding the relationships between completely different metric models. For instance, "kilo" means 1000, so 1 kilometer (km) is the same as 1000 meters (m). Conversely, "milli" means 0.001, so 1 milliliter (ml) is the same as 0.001 liters (l).
II. Models of Size:
The bottom unit for size within the metric system is the meter (m). Different models of size are derived by making use of the prefixes talked about above. This is a chart summarizing frequent size models:
| Unit | Image | Equal in Meters | Typical Makes use of |
|---|---|---|---|
| Kilometer | km | 1000 m | Measuring lengthy distances (e.g., highway distances, geographical distances) |
| Meter | m | 1 m | Measuring reasonable distances (e.g., room dimensions, top) |
| Decimeter | dm | 0.1 m | Much less generally used, typically in specialised fields |
| Centimeter | cm | 0.01 m | Measuring smaller objects (e.g., size of a pencil, width of a e book) |
| Millimeter | mm | 0.001 m | Measuring very small objects (e.g., thickness of a sheet of paper, insect dimension) |
| Micrometer (micron) | µm | 0.000001 m | Measuring microscopic objects (e.g., cell dimension, bacterial dimensions) |
Changing between size models: Changing between these models is simple because of the decimal nature of the system. To transform from a bigger unit to a smaller unit, multiply by the suitable energy of ten. To transform from a smaller unit to a bigger unit, divide by the suitable energy of ten.
- Instance: Convert 2.5 kilometers to centimeters.
1 km = 1000 m
1 m = 100 cm
Due to this fact, 2.5 km = 2.5 km 1000 m/km 100 cm/m = 250,000 cm
III. Models of Quantity:
The bottom unit for quantity is the liter (l), though the cubic meter (m³) can also be broadly used, notably in scientific contexts. The liter is roughly equal to a cubic decimeter (dm³). Widespread quantity models embody:
| Unit | Image | Equal in Liters | Typical Makes use of |
|---|---|---|---|
| Kiloliter | kl | 1000 l | Measuring giant volumes of liquids (e.g., water tanks, swimming swimming pools) |
| Liter | l | 1 l | Measuring reasonable volumes of liquids (e.g., bottles, jugs) |
| Milliliter | ml | 0.001 l | Measuring small volumes of liquids (e.g., medication dosages, cooking measurements) |
| Cubic Meter | m³ | 1000 l | Measuring giant volumes in scientific and engineering functions |
Changing between quantity models: Much like size conversions, changing between quantity models entails multiplying or dividing by powers of ten.
- Instance: Convert 500 milliliters to liters.
1 l = 1000 ml
Due to this fact, 500 ml = 500 ml / 1000 ml/l = 0.5 l
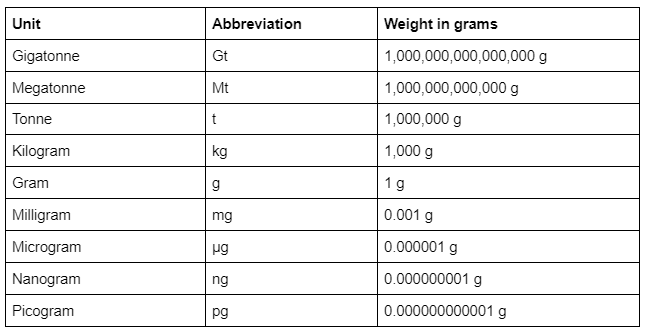
IV. Models of Mass:
The bottom unit for mass is the gram (g). Mass is a measure of the quantity of matter in an object, whereas weight is a measure of the power of gravity on that object. Widespread mass models embody:
| Unit | Image | Equal in Grams | Typical Makes use of |
|---|---|---|---|
| Kilogram | kg | 1000 g | Measuring the mass of bigger objects (e.g., folks, automobiles, groceries) |
| Gram | g | 1 g | Measuring the mass of smaller objects (e.g., meals components, small packages) |
| Milligram | mg | 0.001 g | Measuring very small lots (e.g., medication dosages, scientific experiments) |
Changing between mass models: The conversion course of is similar to the earlier examples.
- Instance: Convert 2.5 kilograms to milligrams.
1 kg = 1000 g
1 g = 1000 mg
Due to this fact, 2.5 kg = 2.5 kg 1000 g/kg 1000 mg/g = 2,500,000 mg
V. Sensible Functions and Significance:
The metric system’s simplicity facilitates ease of use throughout varied disciplines. Its constant use of prefixes makes calculations and conversions easy, lowering errors and bettering effectivity. That is notably essential in fields like science, engineering, medication, and worldwide commerce, the place exact measurements are paramount. The worldwide adoption of the metric system ensures common understanding and avoids the confusion that may come up from utilizing a number of, incompatible techniques. The constant decimal construction simplifies calculations, making it simpler to carry out arithmetic operations and lowering the chance of errors.
Moreover, the metric system’s logical construction promotes higher scientific literacy and understanding of basic ideas. By understanding the relationships between completely different models, people can develop a stronger grasp of measurement ideas and apply this data to numerous elements of life.
VI. Conclusion:
The metric system, with its base models and prefixes, gives a coherent and environment friendly framework for measurement. Understanding the relationships between kilometers, meters, centimeters, and millimeters for size; kiloliters, liters, and milliliters for quantity; and kilograms, grams, and milligrams for mass is essential for navigating on a regular basis life and varied skilled contexts. The convenience of conversion between these models makes the metric system a strong instrument for correct and environment friendly measurement throughout a broad spectrum of functions. Mastering the metric system is crucial for efficient communication and collaboration in a globalized world.




Closure
Thus, we hope this text has supplied beneficial insights into Navigating the Metric System: A Complete Information to Models of Measurement. We thanks for taking the time to learn this text. See you in our subsequent article!