Unveiling The UCL Components For NP Charts: A Deep Dive Into Course of Management

Unveiling the UCL Components for NP Charts: A Deep Dive into Course of Management

Associated Articles: Unveiling the UCL Components for NP Charts: A Deep Dive into Course of Management

Introduction

With nice pleasure, we are going to discover the intriguing matter associated to Unveiling the UCL Components for NP Charts: A Deep Dive into Course of Management. Let’s weave fascinating info and supply recent views to the readers.

Unveiling the UCL Components for NP Charts: A Deep Dive into Course of Management

The Nelson-Course of Functionality (NPC) chart, usually shortened to easily the NP chart, is a strong statistical course of management (SPC) software used to watch the variety of nonconforming models in a pattern of fixed measurement. In contrast to p-charts which observe the proportion of nonconforming models, NP charts concentrate on the depend of defects, making them significantly helpful when the pattern measurement stays constant all through the method. Understanding the higher management restrict (UCL) system for NP charts is essential for efficient course of monitoring and enchancment. This text will delve into the intricacies of this system, exploring its derivation, software, and the essential concerns for its correct and efficient use.

Understanding the Fundamentals: NP Chart Fundamentals

Earlier than diving into the UCL system, let’s set up a foundational understanding of NP charts. These charts are employed when:

• Pattern measurement (n) stays fixed: That is the defining attribute of an NP chart. Every pattern taken for inspection comprises the identical variety of models.
• The method attribute is the variety of nonconforming models: We have an interest within the precise depend of faulty gadgets, not the proportion.
• The information are discrete: The variety of nonconforming models can solely take integer values (0, 1, 2, …).

The NP chart consists of three key traces:

• Middle Line (CL): Represents the common variety of nonconforming models.
• Higher Management Restrict (UCL): The higher boundary past which the method is taken into account statistically uncontrolled. Factors plotting above this restrict counsel a possible enhance in defects.
• Decrease Management Restrict (LCL): The decrease boundary beneath which the method is taken into account statistically uncontrolled. Factors plotting beneath this restrict counsel a possible lower in defects (though that is much less widespread and sometimes signifies a distinct kind of downside).

Deriving the UCL Components: A Statistical Method

The UCL for an NP chart is derived from the binomial distribution, which governs the likelihood of observing a particular variety of successes (nonconforming models on this case) in a hard and fast variety of trials (pattern measurement). Whereas the precise binomial distribution can be utilized, the traditional approximation is commonly employed attributable to its computational simplicity, particularly when the pattern measurement is massive. This approximation is legitimate when each np and n(1-p) are larger than 5, the place n is the pattern measurement and p is the proportion of nonconforming models.

The system for the UCL utilizing the traditional approximation is:

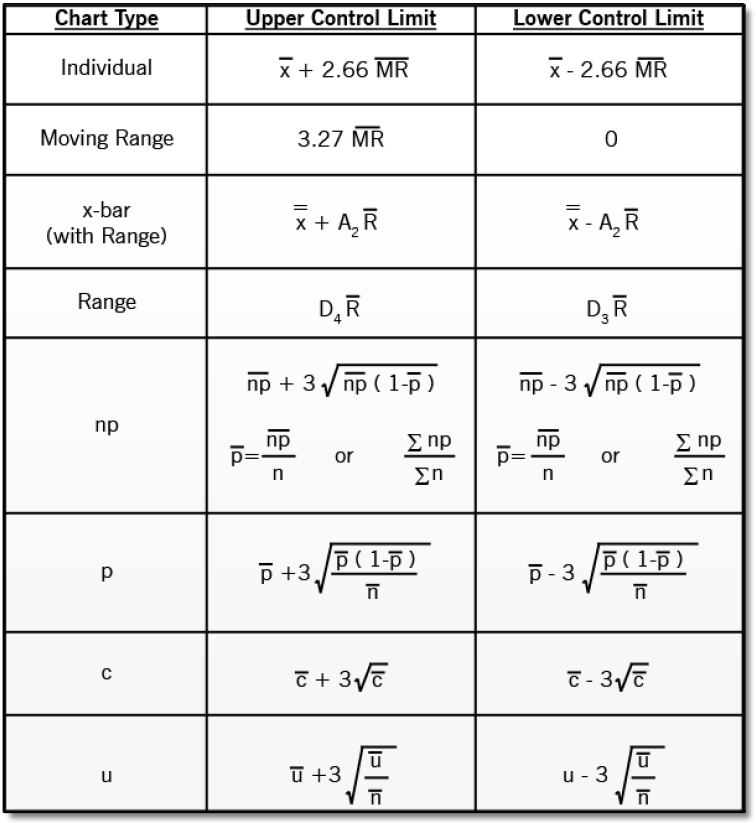
UCL = np + 3√(np(1-p))

The place:

• n: The fixed pattern measurement.
• p: The estimated proportion of nonconforming models. That is calculated from the historic knowledge, sometimes the common proportion of nonconforming models from a considerable variety of samples. That is calculated as: p = Σ(variety of nonconforming models in every pattern) / (variety of samples * n)

The ‘3’ within the system represents three customary deviations from the imply, a standard alternative in SPC to supply a 99.73% confidence degree that factors inside the management limits characterize widespread trigger variation. Factors outdoors this restrict counsel the presence of particular trigger variation, requiring investigation.

Estimating ‘p’: The Significance of Historic Information

The accuracy of the UCL closely depends on the correct estimation of ‘p’. This necessitates a ample quantity of historic knowledge collected beneath secure course of circumstances. A small or poorly consultant dataset will result in inaccurate management limits, doubtlessly masking true course of shifts or falsely indicating out-of-control conditions.

Ideally, a minimum of 20-25 subgroups (samples) needs to be used to estimate ‘p’ to make sure a dependable estimate. If fewer subgroups can be found, different strategies like Bayesian approaches is likely to be thought of to include prior information or professional judgment. The number of historic knowledge is essential; knowledge from intervals recognized to have skilled vital course of adjustments needs to be excluded.

Deciphering the UCL: Recognizing Out-of-Management Alerts

As soon as the UCL is calculated, the NP chart could be constructed. Every new pattern’s variety of nonconforming models is plotted on the chart. Factors persistently falling above the UCL point out a possible enhance in defects, suggesting particular trigger variation. This is likely to be attributable to components equivalent to:

• Machine malfunction: Tools failure or miscalibration.
• Uncooked materials variation: Adjustments within the high quality of incoming supplies.
• Operator error: Inconsistent procedures or lack of coaching.
• Environmental components: Temperature, humidity, or different environmental adjustments.

Investigating these potential causes is essential to deal with the underlying points and restore the method to a state of management.

Past the UCL: The Full NP Chart

Whereas the UCL is a important element, the whole NP chart additionally consists of the CL and LCL. The formulation are:

• CL = np
• LCL = np – 3√(np(1-p)) (Observe: LCL could be destructive; in such circumstances, it’s sometimes set to 0)

The LCL represents a decrease certain, although its interpretation is commonly much less important than the UCL. Some extent beneath the LCL would possibly point out an unexpectedly low variety of defects, which may very well be attributable to components like overly stringent inspection or a brief enchancment that isn’t sustainable.

Issues and Limitations:

• Fixed Pattern Measurement: The NP chart’s validity hinges on sustaining a continuing pattern measurement. Variations in pattern measurement necessitate the usage of p-charts as a substitute.
• Independence of Samples: The information factors plotted on the NP chart ought to characterize impartial samples. If samples are taken sequentially and correlated, the management limits may not be correct.
• Regular Approximation: The traditional approximation used within the UCL system is legitimate solely when np and n(1-p) are larger than 5. For smaller pattern sizes or proportions, the precise binomial distribution needs to be used, though that is computationally extra intensive.
• Course of Stability: The accuracy of the management limits depends on the idea that the method is secure throughout the interval when the historic knowledge was collected. If the method was unstable, the ensuing management limits will probably be deceptive.

Conclusion:

The UCL system for NP charts is a crucial element in statistical course of management. Understanding its derivation, software, and limitations is crucial for successfully monitoring and bettering processes the place the variety of nonconforming models in a continuing pattern measurement is the important thing efficiency indicator. By fastidiously choosing historic knowledge, appropriately calculating the management limits, and correctly deciphering the ensuing charts, organizations can leverage the facility of NP charts to establish and tackle course of variations, resulting in improved product high quality and decreased waste. Bear in mind, nonetheless, that the NP chart is a software, and its efficient use requires a radical understanding of statistical ideas and a dedication to steady course of enchancment. Combining the NP chart with different high quality management instruments and a robust understanding of the method itself will result in the simplest outcomes.

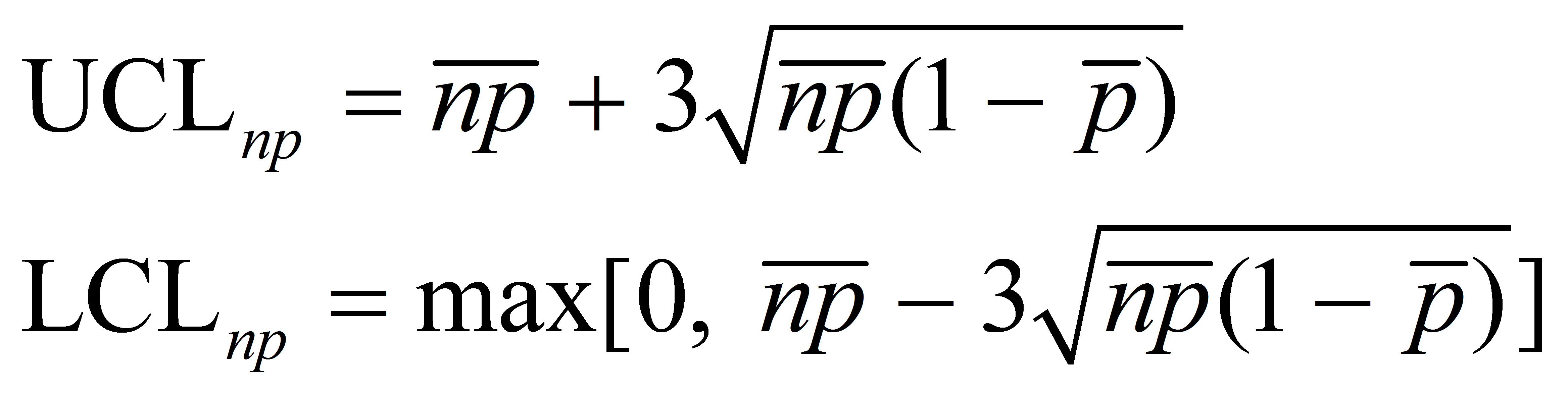
Closure

Thus, we hope this text has supplied invaluable insights into Unveiling the UCL Components for NP Charts: A Deep Dive into Course of Management. We hope you discover this text informative and helpful. See you in our subsequent article!